多层感知机:分类问题
CIFAR-10数据集是深度学习中常用的数据集,其包含60000张32×32色图像,分为10个类,每类6000张。有50000张训练图片和10000张测试图片。
请基于该数据集搭建包含三个及以上的卷积层的多层感知机网络,以解决10分类问题。
(1) 输出网络结构;(1分)
(2) 使用tensorboard对训练过程中的loss和accuracy进行可视化展示;(2分)
(3) 保存训练模型为模型文件,并使用训练好的模型对测试集中的图片进行预测,输出预测结果与预测概率;(2分)
(4) 画出训练集和验证集的混淆矩阵;(2分)
(5) 分析网络参数(例如网络深度、不同的激活函数、神经元数量等)对预测结果的影响;(2分)
(6) 在损失函数为交叉熵的情况下,对比网络最后一层是否使用softmax的性能差异并分析其产生的原因。(1分)
核心任务:使用 CIFAR-10 数据集,搭建一个卷积神经网络 (CNN) 来解决10分类的图像问题。
注意:题目中写的是“多层感知机网络”,但紧接着要求“包含三个及以上的卷积层”。这是一个典型的卷积神经网络 (CNN) 任务,而不是传统意义上只包含全连接层的多层感知机 (MLP)。MLP直接处理拉平的图像向量效果会很差,使用CNN是正确的解法
内容要求分解
- (1) 输出网络结构:
- 要求:展示你设计的网络结构
- 做什么:使用 PyTorch (torch.nn.Module) 或 TensorFlow (tf.keras.Model) 定义一个CNN模型。这个模型必须至少包含3个卷积层 (nn.Conv2d)。一个经典的结构是 (Conv -> ReLU -> Pool) * N -> Flatten -> Linear -> ReLU -> Linear
- 实验报告中要写什么:在代码中 print(your_model),将打印出的网络结构文本复制到报告中。也可以使用 torchsummary 等库来更详细地展示
- (2) TensorBoard 可视化:
- 要求:使用 TensorBoard 展示训练过程中的 loss 和 accuracy
- 做什么:
- 在 PyTorch 中,使用 from torch.utils.tensorboard import SummaryWriter
- 在训练循环中,记录每个 epoch 或每个 batch 的训练/验证 loss 和 accuracy,并使用 writer.add_scalar() 函数将它们写入日志
- 训练完成后,在命令行启动 tensorboard —logdir=runs (runs是你的日志文件夹),然后将生成的图表截图
- 实验报告中要写什么:粘贴 TensorBoard 中显示的 loss 曲线和 accuracy 曲线的截图
- (3) 模型保存与预测:
- 要求:保存训练好的模型,并用它来预测测试集图片
- 做什么:
- 保存:训练结束后,使用 torch.save(model.state_dict(), ‘cifar10_cnn.pth’) 保存模型参数
- 加载:创建一个新的模型实例,然后使用 model.load_state_dict(torch.load(‘cifar10_cnn.pth’)) 加载参数
- 预测:从测试集中随机挑选几张图片,输入到加载好的模型中。注意要将模型设置为评估模式 model.eval()
- 输出概率:模型输出的是 logits,需要经过 torch.nn.functional.softmax 函数转换成概率分布
- 输出结果:使用 torch.argmax() 从概率分布中找到概率最高的类别作为预测结果
- 实验报告中要写什么:展示几张测试图片,以及模型对它们的预测类别和对应的概率
- (4) 混淆矩阵:
- 要求:画出训练集和验证集的混淆矩阵
- 做什么
- 在整个训练集和验证集上运行预测,收集所有的真实标签和预测标签
- 使用 sklearn.metrics.confusion_matrix 生成混淆矩阵。
- 使用 seaborn.heatmap 或 sklearn.metrics.ConfusionMatrixDisplay 将混淆矩阵可视化。
- 实验报告中要写什么:展示训练集和验证集的混淆矩阵热力图,并可以简要分析一下,比如哪些类别之间容易混淆(例如猫和狗)。
- (5) 网络参数影响分析:
- 要求:分析网络参数(深度、激活函数、神经元数量等)对结果的影响。
- 做什么:这是一个开放性的分析题。你需要进行对比实验。例如:
- 网络深度:设计一个3层的CNN和一个5层的CNN,比较它们的性能。
- 激活函数:将模型中的 ReLU 替换为 LeakyReLU 或 Sigmoid,比较性能。
- 神经元数量:改变全连接层 (nn.Linear) 的隐藏单元数量,或者改变卷积层 (nn.Conv2d) 的输出通道数(滤波器数量),比较性能。
- 实验报告中要写什么:用表格或图表对比不同配置下的模型性能(如最终的测试准确率),并分析原因。例如,更深的网络可能性能更好但也更容易过拟合;Sigmoid 容易导致梯度消失等。
- (6) Softmax 与交叉熵损失函数:
- 要求:对比网络最后一层是否使用 softmax 的性能差异,并分析原因。
- 做什么:
- 实验对比:
- 正确做法:网络最后一层直接输出 logits (无激活函数),损失函数使用 torch.nn.CrossEntropyLoss。
- 错误做法:网络最后一层接一个 nn.Softmax 层,损失函数依然使用 torch.nn.CrossEntropyLoss。
- 训练这两个网络,对比它们的性能。
- 原因分析:这是非常重要的一个知识点。PyTorch 的 CrossEntropyLoss 函数内部已经包含了 LogSoftmax 和 NLLLoss。如果你在模型末尾手动添加了 Softmax,那么在计算损失时就相当于进行了两次 Softmax 操作,这会导致梯度计算不正确,使得模型训练非常缓慢或无法收敛。
- 实验对比:
- 实验报告中要写什么:展示两种做法的性能对比(比如 loss 曲线),并清晰地解释 CrossEntropyLoss 的工作原理,阐明为什么在它的前面不应该加 Softmax 层。
题目分析
使用的CIFAR-10数据集是一个有十个类别的、大小为 3 X 32 X 32。
It has the classes: ‘airplane’, ‘automobile’, ‘bird’, ‘cat’, ‘deer’, ‘dog’, ‘frog’, ‘horse’, ‘ship’, ‘truck’. The images in CIFAR-10 are of size 3x32x32, i.e. 3-channel color images of 32x32 pixels in size.
它包含以下类别:‘飞机’、‘汽车’、‘鸟’、‘猫’、‘鹿’、‘狗’、‘青蛙’、‘马’、‘船’、‘卡车’。CIFAR-10 中的图像尺寸为 3x32x32,即 3 通道彩色图像,每个通道包含 32x32 像素。
题目要求”搭建包含三个及以上的卷积层的多层感知机网络”,指明了实际上要搭建的是一个 三层以上网络的CNN卷积神经网络。
常用的卷积神经网络有:
- LeNet-5: 早期用于手写数字识别的CNN,是现代CNN的鼻祖
- AlexNet: 在 ImageNet 竞赛中取得突破,引爆了深度学习革命
- VGGNet: 展示了通过堆叠小的卷积核(3x3)可以构建出很深很有效的网络
- GoogLeNet: 引入了“Inception模块” ,可以在同一层使用不同尺寸的卷积核
- ResNet: 里程碑式的模型。通过引入残差连接,成功训练了超过100层甚至1000层的超深网络,解决了深度网络的梯度消失和退化问题
对于本题,为方便起见,采用 VGGNet风格来构建特征提取器,结合经典的LeNet-5全连接层结构,实现轻量级的CNN。
(1) 输出网络结构
即三个 “cov → Pool” 的 LeNet-5结构,而每一个卷积层的核为 VGGNet的 “3 x 3”样式,全连接层使用的经典的 LeNet-5 的 “120 → 84 → 10”的结构。
Net(
(conv1): Conv2d(3, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(pool1): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(conv2): Conv2d(16, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(pool2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(conv3): Conv2d(32, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(pool3): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(fc1): Linear(in_features=1024, out_features=120, bias=True)
(fc2): Linear(in_features=120, out_features=84, bias=True)
(fc3): Linear(in_features=84, out_features=10, bias=True)
)(2) 使用tensorboard对训练过程中的loss和accuracy进行可视化展示
相关代码:
# 使用 tensorboard 可视化训练过程
from torch.utils.tensorboard import SummaryWriter
writer = SummaryWriter('./logs')
trained_model,history = train(
model=model,
device=device,
trainloader=trainloader,
loss_function=loss_function,
optimizer=optimizer,
epoches=20,
writer=writer
)
writer.close()
print('结束Summary的写入')结果:
准确率
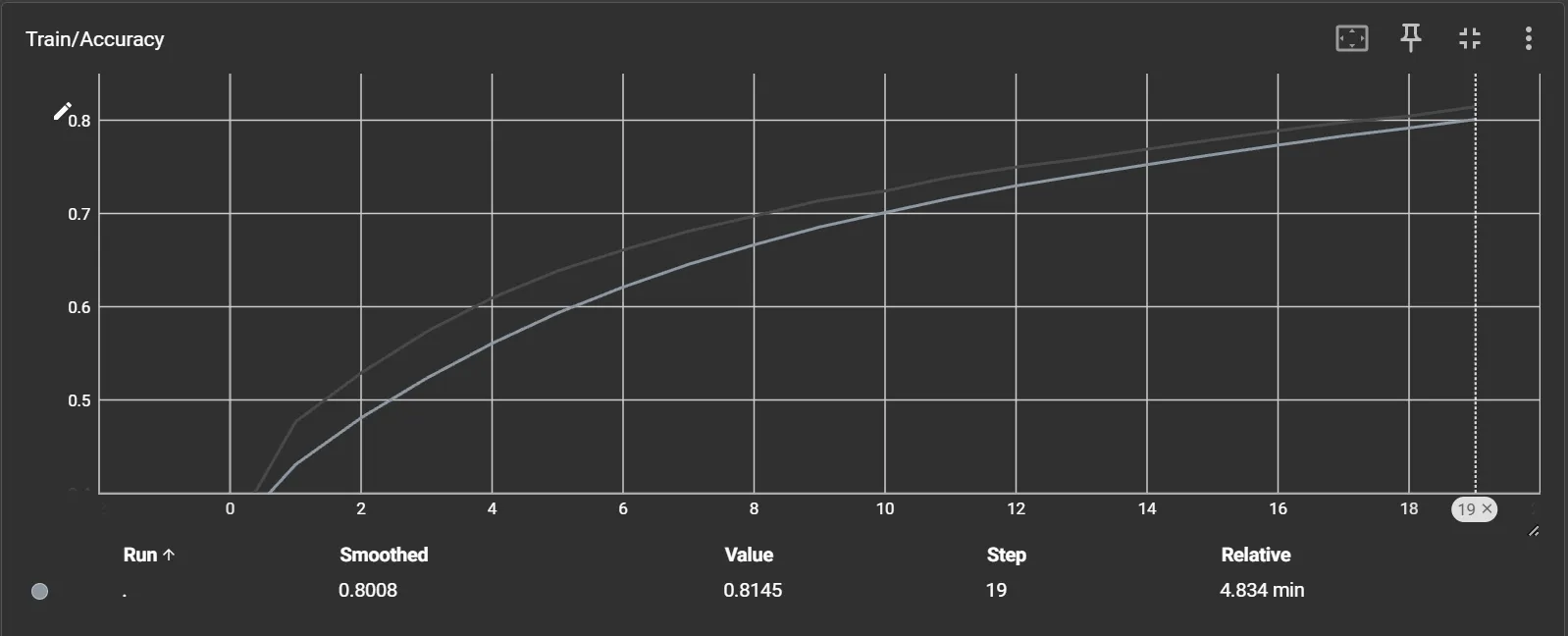
损失值
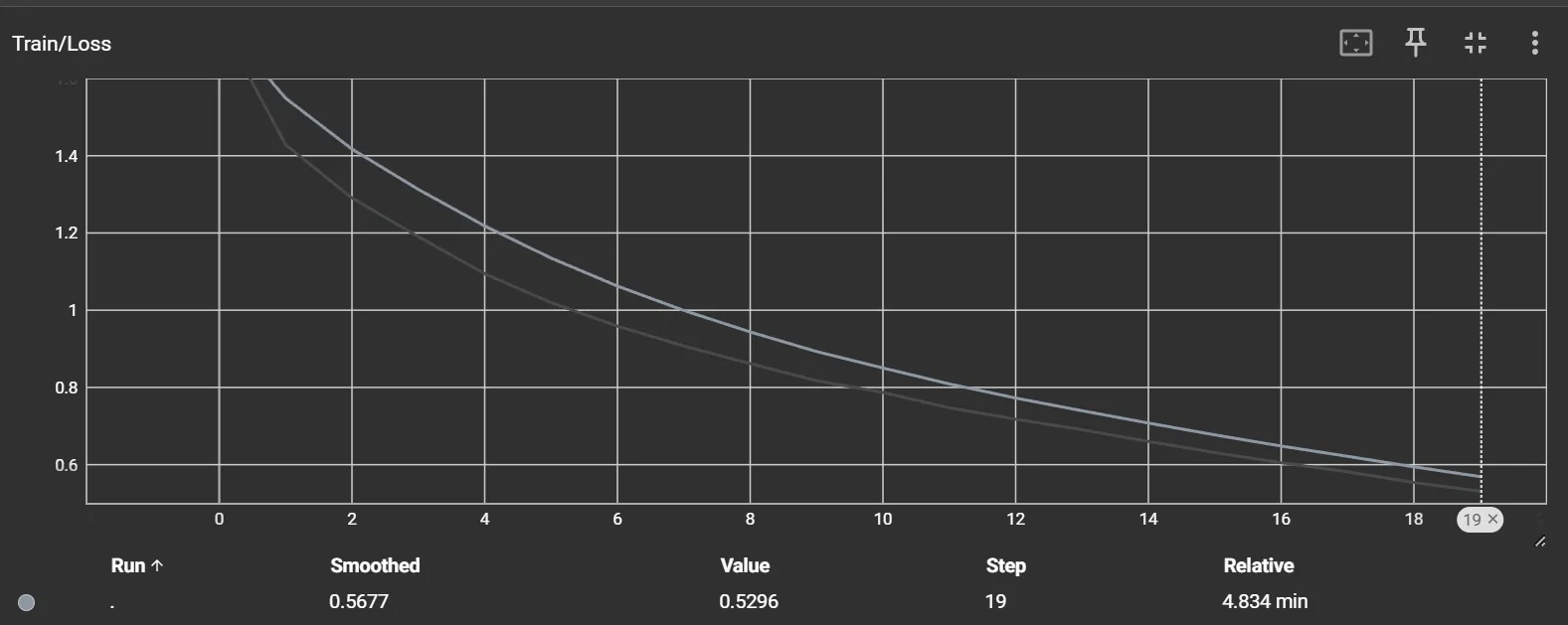
(3) 保存训练模型为模型文件,并使用训练好的模型对测试集中的图片进行预测,输出预测结果与预测概率
3.1.模型持久化
# 模型持久化区块
PATH = './cifar_net.pth'
save_model(trained_model,PATH)3.2. 简单图片预测
# 简单的图像评估区块
def imshow(img):
img = img / 2 + 0.5 # 反标准化
npimg = img.numpy()
plt.imshow(np.transpose(npimg, (1, 2, 0)))
plt.show()
data_iter = iter(testloader)
images, labels = next(data_iter)
show_images = 8
images_to_show = images[:show_images]
labels_to_show = labels[:show_images]
print('GroundTruth: ', ' '.join(f'{classes[labels_to_show[j]]:5s}' for j in range(show_images)))
# 使用已持久化模型进行评估
model = Net()
model.load_state_dict(torch.load(PATH, weights_only=True))
# 预测标签
with torch.no_grad():
outputs = model(images_to_show)
_, predicted = torch.max(outputs, 1)
print('Predicted: ', ' '.join(f'{classes[predicted[j]]:5s}' for j in range(show_images)))
imshow(torchvision.utils.make_grid(images_to_show))结果:
GroundTruth: cat ship ship plane frog frog car frog
Predicted: cat ship ship plane frog frog car deer 
3.3. 测试集整体准确率预测
model = Net()
model.load_state_dict(torch.load(PATH, weights_only=True))
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
test_accuracy = pred_model(
model=model,
testloader=testloader,
device=device
)
print(f'测试集准确率:{test_accuracy*100:.2f}%')结果:
测试集准确率:71.46%3.4. 各类别的准确率预测
correct_pred = {classname: 0 for classname in classes}
total_pred = {classname: 0 for classname in classes}
with torch.no_grad():
for data in testloader:
images, labels = data[0].to(device), data[1].to(device)
outputs = model(images)
_, predictions = torch.max(outputs, 1)
# 累加每个类别的准确率计算变量
for label, prediction in zip(labels, predictions):
if label == prediction:
correct_pred[classes[label]] += 1
total_pred[classes[label]] += 1
# print accuracy for each class
for classname, correct_count in correct_pred.items():
accuracy = 100 * float(correct_count) / total_pred[classname]
print(f'Class: {classname:5s} Accuracy: {accuracy:.1f} %')结果:
Class: plane Accuracy: 69.0 %
Class: car Accuracy: 87.0 %
Class: bird Accuracy: 57.0 %
Class: cat Accuracy: 51.6 %
Class: deer Accuracy: 61.1 %
Class: dog Accuracy: 64.2 %
Class: frog Accuracy: 88.0 %
Class: horse Accuracy: 71.9 %
Class: ship Accuracy: 83.5 %
Class: truck Accuracy: 81.3 %(4) 画出训练集和验证集的混淆矩阵
使用 seaborn绘制混淆矩阵
def collect_pred_labels(model, dataloader, device):
"""
遍历 Dataloader,收集模型的所有预测结果和真实标签
:param model: 模型
:param dataloader: 数据加载器
:param device:
:return:
labels:numpy, preds:numpy
"""
labels = torch.tensor([],device=device)
preds = torch.tensor([],device=device)
with torch.no_grad():
for X, y in dataloader:
X,y = X.to(device), y.to(device)
output = model(X)
predicts = output.argmax(dim=1, keepdim=True)
# 拼接当前批次的预测值和标签到列表里
labels = torch.cat((labels,y),dim=0)
preds = torch.cat((preds,predicts),dim=0)
# 直接返回 numpy并转移到cpu上,方便后续 seaborn绘图
return labels.cpu().numpy(), preds.cpu().numpy()
def plot_confusion_matrix(cm, class_names,title='Confusion matrix'):
"""
使用seaborn绘制混淆矩阵
"""
plt.figure(figsize=(10,8))
sns.heatmap(cm,annot=True,fmt='d',cmap='Blues',
xticklabels=class_names,yticklabels=class_names)
plt.title(title)
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.tight_layout()
plt.show()结果:
训练集混淆矩阵

测试集混淆矩阵
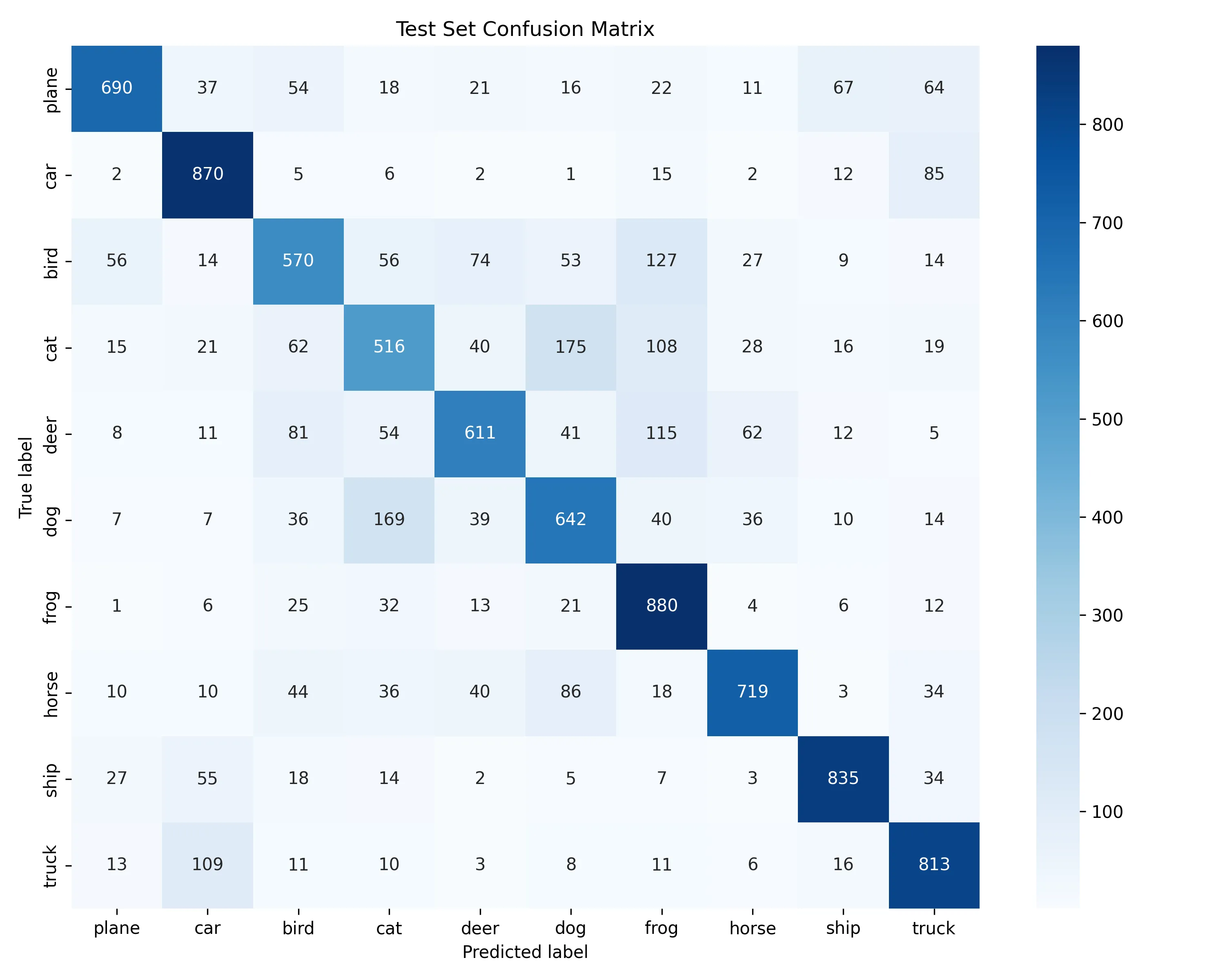
(5) 分析网络参数(网络深度、不同的激活函数、神经元数量)对预测结果的影响
5.1.网络深度对预测结果的影响
三层网络
即当前层数的网络:
Net(
(conv1): Conv2d(3, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(pool1): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(conv2): Conv2d(16, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(pool2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(conv3): Conv2d(32, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(pool3): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(fc1): Linear(in_features=1024, out_features=120, bias=True)
(fc2): Linear(in_features=120, out_features=84, bias=True)
(fc3): Linear(in_features=84, out_features=10, bias=True)
)五层网络
在三层网络的基础再增加两层 “Cov → Pool”的网络结构,将其扩展为五层。对于CIFAR-10数据集,采用 积极下采样的方式即可,若采用延迟下采样,使得输出维度变为 128 x 4 x 4 = 2048,在小型数据集 CIFAR-10中容易造成过拟合。
新的网络结构:
| 层级 | 输出形状 | 空间尺寸 (H x W) | 通道数 (语义深度) |
|---|---|---|---|
| 输入 | [B, 3, 32, 32] | 大 (1024) | 低 (3) |
| 块 1 | [B, 16, 16, 16] | ↓ | ↑ |
| 块 2 | [B, 32, 8, 8] | ↓ | ↑ |
| 块 3 | [B, 64, 4, 4] | ↓ | ↑ |
| 块 4 | [B, 128, 2, 2] | ↓ | ↑ |
| 块 5 | [B, 128, 1, 1] | 极小 (1) | 高 (128) |
每一个块都是:“Cov => Pool”。
Net(
(conv1): Conv2d(3, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(pool1): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(conv2): Conv2d(16, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(pool2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(conv3): Conv2d(32, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(pool3): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(conv4): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(pool4): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(conv5): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(pool5): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(fc1): Linear(in_features=128, out_features=120, bias=True)
(fc2): Linear(in_features=120, out_features=84, bias=True)
(fc3): Linear(in_features=84, out_features=10, bias=True)
)训练过程:
Epoch [19/20] | Train Loss: 0.3948 | Train Accuracy: 0.8601
Epoch [20/20] | Train Loss: 0.3675 | Train Accuracy: 0.8706可以看到训练集准确率高达 0.87,三层网络的训练集准确率为 0.76,低了 0.11。
结果分析
1. 实验结果:
预测结果如下(在测试集上预测):
| 类别 | 三层网络 | 五层网络 |
|---|---|---|
| 平均准确率 | 71.46% | 70.75% |
| plane | 69.0 % | 72.2 % |
| car | 87.0 % | 81.9 % |
| bird | 57.0 % | 55.1 % |
| cat | 51.6 % | 55.5 % |
| deer | 61.1 % | 75.0 % |
| dog | 64.2 % | 67.1 % |
| frog | 88.0 % | 78.5 % |
| horse | 71.9 % | 77.1 % |
| ship | 83.5 % | 67.2 % |
| truck | 81.3 % | 77.9 % |
3层网络的最终测试集准确率为 71.46%,略高于5层网络的 70.75%;这个结果表明,对于本次实验任务,并非简单地增加网络深度就能带来性能的提升。
2. 原因分析:
5层网络性能反而下降的主要原因可能在于过度下采样导致的关键信息丢失:
-
3层网络:
输入图像的尺寸为 32x32,经过三次池化操作后,进入全连接层之前的特征图尺寸为 4x4。在这个尺度下,特征图依然保留了物体部分特征的相对空间位置信息,例如,“车轮”在“车身”的下方。
-
5层网络:
输入图像同样为 32x32,但经过了五次池化操作,最终进入全连接层之前的特征图尺寸被压缩至 1x1。这意味着所有空间维度的信息都已丢失,网络只知道图像中“有些特征,但完全丢失了这些特征的排布和结构信息。
5层网络过于激进的空间压缩,可能破坏了区分不同类别所必需的结构化信息,形成了一个信息瓶颈,从而限制了模型的最终性能。
除了过采样问题,还可能是由于反向传播路径较长出现了 梯度消失的问题,以及 过拟合风险。
综合来看,对于CIFAR-10数据集(32x32像素),3层卷积网络在模型的表达能力、信息保留和训练难度之间取得了更好的平衡。而5层网络虽然理论上更强大,但其结构设计中的过度下采样破坏了对分类任务至关重要的空间信息,同时增加了训练的难度和过拟合的风险,最终导致了性能的轻微下降。
5.2. 不同的激活函数对预测结果的影响
由前文,对于该数据集,五层效果和三层差不多,甚至更差,因此在 5.2. 和 5.3. 中,采用三层的神经网络;并由于 20轮训练时间较久,观察训练的每一轮的损失值和准确率,第十轮相对而言足够。
train accuracy :0.71504 | train loss:0.798097129379本节对比三种激活函数:
- ReLU
- LeakyReLU
- Sigmoid
预测结果如下(在测试集上预测):
| 类别 | ReLU | LeakyReLU | Sigmoid |
|---|---|---|---|
| 平均准确率 | 68.43% | 70.86% | 49.01% |
| plane | 73.0 % | 73.2 % | 48.8 % |
| car | 77.5 % | 77.6 % | 66.7 % |
| bird | 49.5 % | 68.4 % | 29.3 % |
| cat | 45.4 % | 49.4 % | 30.8 % |
| deer | 59.3 % | 55.5 % | 46.9 % |
| dog | 69.2 % | 63.4 % | 32.1 % |
| frog | 84.8 % | 84.0 % | 59.8 % |
| horse | 74.2 % | 74.5 % | 62.4 % |
| ship | 77.8 % | 82.8 % | 60.7 % |
| truck | 73.6 % | 79.8 % | 52.6 % |
结果分析:
整体分析
| 激活函数 | 整体测试集准确率 | 性能排序 |
|---|---|---|
| LeakyReLU | 70.86% | 最佳 |
| ReLU | 68.43% | 良好 |
| Sigmoid | 49.01% | 较差 |
ReLU 和 LeakyReLU 两种激活函数均表现出色,整体准确率分别达到了68.43%和70.86%,远超Sigmoid函数。这主要得益于它们有效缓解了深度网络中常见的梯度消失问题。当输入信号为正时,ReLU和LeakyReLU的导数恒为1,这保证了梯度在反向传播过程中可以顺畅地流过激活的神经元,使得网络能够进行有效学习。
从各类别准确率来看,LeakyReLU在ReLU表现较差的类别上提升尤为明显,例如 ‘bird’(从49.5%提升至68.4%)和 ‘dog’(从69.2%降至63.4%,此处为个例,但总体提升显著),这表明LeakyReLU的鲁棒性可能更强,帮助模型学习到了更难区分的特征。
Sigmoid激活函数的模型表现最差,整体准确率仅为49.01%,远低于前两者。这清晰地暴露了Sigmoid函数在深度网络中的固有缺陷,即梯度饱和与梯度消失问题。
5.3. 神经元数量对预测结果的影响
5.3.1. 改变卷积层神经元数量
将网络的维度:16 -> 32 -> 64 变为 32->64->128,使神经网络更加地宽,进而使其有能力学习更多的特征。
使用的损失函数为 LeakyReLU。
1. 低维:16 -> 32 -> 64
2. 高维:32->64->128
-
网络结构:
Net( (conv1): Conv2d(3, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (pool1): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False) (conv2): Conv2d(32, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (pool2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False) (conv3): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (pool3): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False) (fc1): Linear(in_features=2048, out_features=120, bias=True) (fc2): Linear(in_features=120, out_features=84, bias=True) (fc3): Linear(in_features=84, out_features=10, bias=True) ) -
训练输出
Epoch [9/10] | Train Loss: 0.4902 | Train Accuracy: 0.8282 Epoch [10/10] | Train Loss: 0.4309 | Train Accuracy: 0.8495可以看到,加宽卷积层后,训练损失和准确率都达到了很好的状态,性能比低维度时好了许多。
3. 结果分析:
| 类别 | 低维 | 高维 |
|---|---|---|
| 平均准确率 | 70.86% | 75.41% |
| plane | 73.2 % | 84.4 % |
| car | 77.6 % | 85.8 % |
| bird | 68.4 % | 59.3 % |
| cat | 49.4 % | 56.6 % |
| deer | 55.5 % | 71.5 % |
| dog | 63.4 % | 68.3 % |
| frog | 84.0 % | 81.7 % |
| horse | 74.5 % | 72.8 % |
| ship | 82.8 % | 87.4 % |
| truck | 79.8 % | 86.3 % |
将网络加宽(增加卷积层的神经元/通道数)后,模型的平均准确率从70.86%提升至75.41%,获得了4.55%的显著增长。
按照类别查看:
-
提升显著的类别
类别 准确率的增长率 plane +11.2% car +8.2% deer +16.0% ship +4.6% truck +6.5% 这些类别通常具有相对固定和明确的结构特征。
例如飞机有机翼,汽车/卡车有轮子和车窗,船有船体。这些物体的轮廓和关键部件在不同样本间的一致性较高。
-
提升不明显的类别
类别 准确率的增长率 bird - 9.1% frog - 2.3% horse - 1.7% bird 是一个典型的类内差异巨大的类别。
鸟有各种姿态(飞翔、站立)、各种大小(麻雀、鹰)、各种颜色,并且常常与复杂的背景(树林、天空)融为一体。高维网络可能在训练中过拟合了某些特定类型的鸟(比如,训练集中某种背景下的鸟),反而降低了对其他类型鸟的泛化能力。
-
稳定提升的类别
类别 准确率的增长率 cat + 7.2% dog + 4.9% 猫和狗是CIFAR-10中著名的难题,因为它们类间相似性高,且同样存在姿态、品种等类内差异。
高维网络带来的性能提升,说明增加的容量确实帮助模型学习到了区分猫狗的更细微的特征,例如耳朵的形状、鼻子的轮廓等。虽然提升了,但它们的绝对准确率仍然不高。
5.3.2. 改变全连接层神经元数量
全连接层影响网络最后的分类决策部分。
原始全连接层神经元数: 1024 -> 120 -> 84 -> 10,现修改为更大的全连接层神经元数:1024 -> 256 -> 128 -> 10。
1. 原始网络:
Net(
(conv1): Conv2d(3, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(pool1): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(conv2): Conv2d(16, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(pool2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(conv3): Conv2d(32, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(pool3): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(fc1): Linear(in_features=1024, out_features=120, bias=True)
(fc2): Linear(in_features=120, out_features=84, bias=True)
(fc3): Linear(in_features=84, out_features=10, bias=True)
)2. 更大的全连接层网络:
Net(
(conv1): Conv2d(3, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(pool1): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(conv2): Conv2d(16, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(pool2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(conv3): Conv2d(32, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(pool3): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(fc1): Linear(in_features=1024, out_features=256, bias=True)
(fc2): Linear(in_features=256, out_features=128, bias=True)
(fc3): Linear(in_features=128, out_features=10, bias=True)
)训练过程输出:
Epoch [9/10] | Train Loss: 0.6513 | Train Accuracy: 0.7714
Epoch [10/10] | Train Loss: 0.5971 | Train Accuracy: 0.78973. 结果分析:
| 类别 | 原始网络 | 宽全连接层 |
|---|---|---|
| 平均准确率 | 70.86% | 72.77% |
| plane | 73.2 % | 77.0 % |
| car | 77.6 % | 88.0 % |
| bird | 68.4 % | 58.2 % |
| cat | 49.4 % | 49.1 % |
| deer | 55.5 % | 64.3 % |
| dog | 63.4 % | 60.6 % |
| frog | 84.0 % | 78.5 % |
| horse | 74.5 % | 85.3 % |
| ship | 82.8 % | 85.6 % |
| truck | 79.8 % | 81.1 % |
从实验结果的核心指标来看,宽连接层网络取得了更好的整体性能。
- 原始网络平均准确率: 70.86%
- 宽连接层网络平均准确率: 72.77%
这带来了 1.91% 的净准确率提升,是一个较小的改进。
原因分析:
全连接层负责将卷积层提取出的高级特征(如物体的部件、纹理等)进行组合,并最终映射到具体的类别上。通过将全连接层的神经元数量从 (120, 84) 增加到 (256, 128),模型的容量显著的增加了。
结论:
- 增加全连接层宽度是有效的: 从总体结果看,增加分类头的容量成功提升了模型的平均性能,证明原始网络的分类部分确实存在一定的表达能力瓶颈。
- 存在明显的权衡: 模型的总体精力是有限的。更宽的网络将更多的注意力和参数用于学习区分那些特征明显的类别,这在一定程度上牺牲了对那些形态多变、难以定义的类别的泛化能力。
- 参数量与过拟合风险: 宽连接层网络拥有更多的参数,这意味着它需要更多的计算资源进行训练,并且有过拟合的风险。虽然在本次实验中整体效果是正向的,但如果进一步增加宽度或在更小的数据集上训练,性能很可能会因严重的过拟合而下降。
(6) 在损失函数为交叉熵的情况下,对比网络最后一层是否使用softmax的性能差异并分析其产生的原因
1.原始网络
原始网络结构为:
Net(
(conv1): Conv2d(3, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(pool1): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(conv2): Conv2d(16, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(pool2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(conv3): Conv2d(32, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(pool3): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(fc1): Linear(in_features=1024, out_features=120, bias=True)
(fc2): Linear(in_features=120, out_features=84, bias=True)
(fc3): Linear(in_features=84, out_features=10, bias=True)
)查看末尾便可发现原始网络是直接输出 logits的,因为PyTorch 的交叉熵损失函数自带了 Softmax,此时在网络末尾再添加 Softmax会导致计算出的梯度值太过微弱,模型根本无法学习。
训练的损失、准确率曲线:
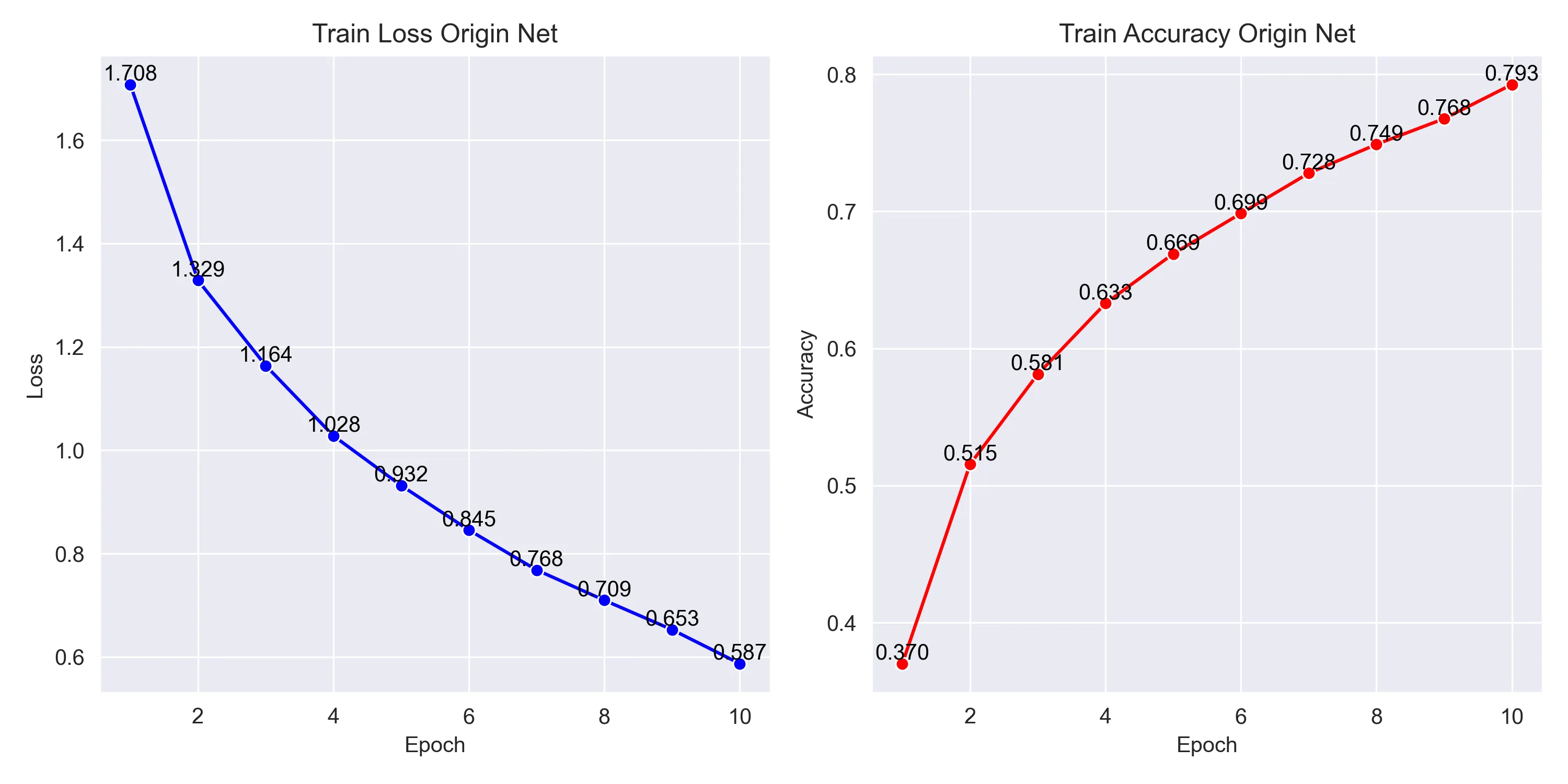
2.最后一层添加了softmax的网络
前向传播顺序:
def forward(self, x):
# 顺序通过卷积块
x = self.pool1(F.leaky_relu(self.conv1(x)))
x = self.pool2(F.leaky_relu(self.conv2(x)))
x = self.pool3(F.leaky_relu(self.conv3(x)))
x = torch.flatten(x, 1)
# 全连接层
x = F.leaky_relu(self.fc1(x))
x = F.leaky_relu(self.fc2(x))
x = self.fc3(x)
x = F.softmax(x, dim=1) # ! 末尾添加softmax
return x训练的损失、准确率曲线:
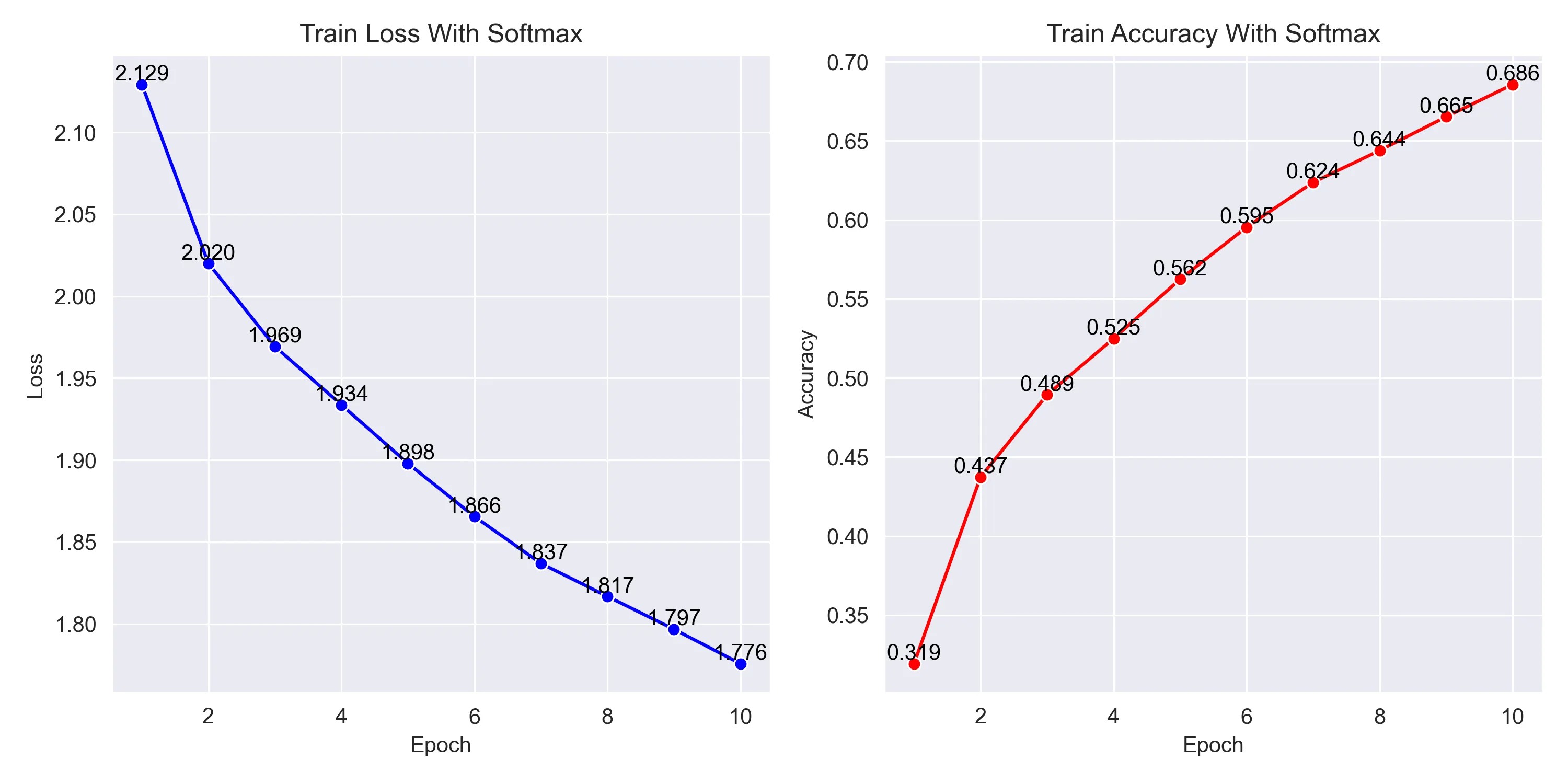
3. 结果分析:
预测结果:
| 类别 | 最后一层不加softmax | 最后一层加softmax |
|---|---|---|
| 平均准确率 | 71.84% | 64.30% |
| plane | 69.0 % | 71.4 % |
| car | 82.2 % | 81.6 % |
| bird | 54.3 % | 58.5 % |
| cat | 43.5 % | 53.5 % |
| deer | 65.9 % | 56.8 % |
| dog | 62.8 % | 37.8 % |
| frog | 88.7 % | 75.0 % |
| horse | 79.1 % | 71.2 % |
| ship | 87.8 % | 84.2 % |
| truck | 85.1 % | 53.0 % |
实验结果清晰地表明,不使用Softmax激活函数(直接输出logits)的网络在各项性能指标上均显著优于使用Softmax的网络。
-
训练过程分析(根据 loss曲线和 accuracy曲线):
-
损失值曲线:
-
初始损失与收敛速度:
A. 不加 Softmax (正确模型): 训练从一个相对较低的损失值 (≈1.71) 开始,并且在前几个epoch中迅速下降,表现出高效的学习效率。
B. 加 Softmax (错误模型): 训练从一个非常高的损失值 (≈2.13) 开始,且下降速度极为缓慢。这表明模型在初始阶段就接收到了非常微弱或不正确的梯度信号,导致学习困难。
-
最终损失:
A. 不加 Softmax: 经过10个 epoch,损失值稳定下降到了约0.66,说明模型较好地拟合了训练数据。
B. 加 Softmax: 10个 epoch后,损失值仍然高达约1.78,几乎没有得到有效的优化。
-
-
训练集准确率曲线:
- 不加 Softmax: 训练准确率从37%开始,稳步且快速地提升,最终达到了接近80% (0.793) 的高水平。
- 加 Softmax: 训练准确率从约32%开始,提升速度缓慢,最终仅达到68.6%,远低于正确模型的水平。这证明了无效的损失函数导致模型无法充分学习训练集中的特征。
综合训练曲线来看,在最后一层添加 Softmax函数的模型表现出明显的学习障碍,其损失函数很难被优化,从而导致准确率提升乏力。
-
-
测试集性能分析:
训练过程中的差异最终体现在模型对未知数据的泛化能力上。
- 平均准确率:
- 不加 Softmax的正确模型在测试集上达到了**71.84%**的平均准确率。
- 加 Softmax的错误模型的平均准确率仅为64.30%。
- 两者相差超过7.5%,这是一个巨大的性能鸿沟,决定性地证明了正确做法的优越性。
- 分项准确率:
- 优势类别:正确模型在大多数类别上都取得了更好的性能,尤其是在 dog (62.8% vs 37.8%)、truck (85.1% vs 53.0%)和 frog (88.7% vs 75.0%) 这几个类别上,领先优势非常明显。
- 异常类别:有趣的是,错误模型在 bird和 cat等少数几个类别上的准确率略高于正确模型。这可能是由于训练过程中的随机性,或是被扭曲的梯度恰好在某些批次的数据上对这几个类别的特征产生了微弱的有利影响。但这并不能改变其整体性能远逊于正确模型的事实。
- 平均准确率:
-
原因分析:
是 torch.nn.CrossEntropyLoss 函数的核心工作原理:PyTorch内置的交叉熵损失函数会对收到的 logits 进行一次 LogSoftmax,将其转换为对数概率;然后使用NLLLoss计算最终的损失值。
因此,交叉熵损失函数本身就使用了 Softmax,如果再重复使用 Softmax,会导致参数数值再度被压缩,进而使梯度信号接近于0,即梯度消失。
源码(可忽略)
import pandas as pd
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
from torchvision import transforms
from torch.utils.data import DataLoader, random_split, Dataset
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import torch.nn.functional as F
def get_dataloader_workers():
"""使用 4 个进程读取数据"""
return 4
class Net(nn.Module):
def __init__(self):
super().__init__()
# 初始输入: [B, 3, 32, 32]
# 第1个卷积块
self.conv1 = nn.Conv2d(3, 16, 3, padding=1) # 输出: [B, 16, 32, 32]
self.pool1 = nn.MaxPool2d(2, 2) # 输出: [B, 16, 16, 16]
# 第2个卷积块
self.conv2 = nn.Conv2d(16, 32, 3, padding=1) # 输出: [B, 32, 16, 16]
self.pool2 = nn.MaxPool2d(2, 2) # 输出: [B, 32, 8, 8]
# 第3个卷积块
self.conv3 = nn.Conv2d(32, 64, 3, padding=1) # 输出: [B, 64, 8, 8]
self.pool3 = nn.MaxPool2d(2, 2) # 输出: [B, 64, 4, 4]
# # 第四个卷积块
# self.conv4 = nn.Conv2d(64, 128, 3, padding=1) # 输出: [B, 128, 4, 4]
# self.pool4 = nn.MaxPool2d(2, 2) # 输出: [B, 64, 2, 2]
#
# # 第五个卷积块
# self.conv5 = nn.Conv2d(128, 128, 3, padding=1) # 输出: [B, 256, 2, 2]
# self.pool5 = nn.MaxPool2d(2, 2) # 输出: [B, 256, 1, 1]
# 全连接层
# 经过 3次池化后,特征图大小为 4x4,通道数为64
# 因此 flatten后的向量维度是 64 * 4 * 4 = 1024
# ------------------------------------------
# 经过 5次池化后,特征图大小为 1x1,通道数为256
# 因此,flatten后的向量维度是 256
self.fc1 = nn.Linear(64 * 4 * 4, 256)
self.fc2 = nn.Linear(256, 128)
self.fc3 = nn.Linear(128, 10)
def forward(self, x):
# 顺序通过卷积块
x = self.pool1(F.leaky_relu(self.conv1(x)))
x = self.pool2(F.leaky_relu(self.conv2(x)))
x = self.pool3(F.leaky_relu(self.conv3(x)))
# x = self.pool4(F.relu(self.conv4(x)))
# x = self.pool5(F.relu(self.conv5(x)))
# 将所有维度展平成一维
x = torch.flatten(x, 1)
# 全连接层
x = F.leaky_relu(self.fc1(x))
x = F.leaky_relu(self.fc2(x))
x = self.fc3(x)
x = F.softmax(x, dim=1)
return x
def train(model, device, trainloader, loss_function, optimizer, epoches, writer):
"""模型训练"""
"""
return:
model trained, history of training loss and training accuracy
"""
model = model.to(device)
history = {'train_loss': [], 'train_accuracy': []}
# 切换为训练模式
model.train()
for epoch in range(epoches):
train_loss = 0.0
acc_cnt = 0
for X,y in trainloader:
# get the inputs; data is a list of [inputs, labels]
X,y = X.to(device), y.to(device)
# 清零梯度
optimizer.zero_grad()
# 前向传播
outputs = model(X)
# 计算loss
loss = loss_function(outputs, y)
loss.backward()
# 更新权重
optimizer.step()
train_loss += loss.item()
acc_cnt += (outputs.argmax(1) == y).type(torch.float).sum().item()
train_loss = train_loss / len(trainloader)
accuracy = acc_cnt / len(trainloader.dataset)
print(f"Epoch [{epoch + 1}/{epoches}] | "
f"Train Loss: {train_loss:.4f} | "
f"Train Accuracy: {accuracy:.4f}")
history['train_loss'].append(train_loss)
history['train_accuracy'].append(accuracy)
# 在每个 epoch 结束后,使用 writer 记录 loss 和 accuracy
# writer.add_scalar(tag, scalar_value, global_step)
# tag: 图表的标题
# scalar_value: y轴的值
# global_step: x轴的值
writer.add_scalar('Train/Loss', train_loss, epoch)
writer.add_scalar('Train/Accuracy', accuracy, epoch)
print('训练完毕')
return model,history
def save_model(model, path):
torch.save(model.state_dict(), path)
print('Save Successfully')
def pred_model_in_testset(model, testloader, device):
"""在测试集上评测最终模型性能"""
model = model.to(device)
model.eval()
acc_cnt = 0
with torch.no_grad():
for X, y in testloader:
X,y = X.to(device), y.to(device)
output = model(X)
acc_cnt += (output.argmax(1) == y).type(torch.float).sum().item()
accuracy = acc_cnt / len(testloader.dataset)
return accuracy
def collect_pred_labels(model, dataloader, device):
"""
遍历 Dataloader,收集模型的所有预测结果和真实标签
:param model: 模型
:param dataloader: 数据加载器
:param device:
:return:
labels:numpy, preds:numpy
"""
labels = torch.tensor([],device=device)
preds = torch.tensor([],device=device)
with torch.no_grad():
for X, y in dataloader:
X,y = X.to(device), y.to(device)
output = model(X)
predicts = output.argmax(dim=1, keepdim=True)
# 拼接当前批次的预测值和标签到列表里
labels = torch.cat((labels,y),dim=0)
preds = torch.cat((preds,predicts),dim=0)
# 直接返回 numpy并转移到cpu上,方便后续 seaborn绘图
return labels.cpu().numpy(), preds.cpu().numpy()
def plot_confusion_matrix(cm, class_names, img_name, title='Confusion matrix'):
"""
使用seaborn绘制混淆矩阵
"""
plt.figure(figsize=(10,8))
sns.heatmap(cm,annot=True,fmt='d',cmap='Blues',
xticklabels=class_names,yticklabels=class_names)
plt.title(title)
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.tight_layout()
plt.savefig(f'{img_name}_CM.png',dpi=300)
plt.show()
def display_confusion_matrix(PATH):
# ========= 绘制训练集和验证集的混淆矩阵 ==============
batch_size = 256
# 数据加载区块
trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
download=True, transform=transform)
testset = torchvision.datasets.CIFAR10(root='./data', train=False,
download=True, transform=transform)
# shuffle = False 以保持顺序
trainloader = torch.utils.data.DataLoader(trainset, batch_size=batch_size,
shuffle=False, num_workers=get_dataloader_workers())
testloader = torch.utils.data.DataLoader(testset, batch_size=batch_size,
shuffle=False, num_workers=get_dataloader_workers())
classes = ('plane', 'car', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
model = Net()
model.load_state_dict(torch.load(PATH, weights_only=True))
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model.to(device)
from sklearn.metrics import confusion_matrix
# 绘制训练集的混淆矩阵
print('训练集混淆矩阵绘制:')
train_labels, train_preds = collect_pred_labels(model, trainloader, device)
cm_train = confusion_matrix(train_labels, train_preds)
plot_confusion_matrix(cm=cm_train,
class_names=classes,
title='Train Set Confusion Matrix',
img_name='train_set')
# 绘制测试集的混淆矩阵
print('测试集混淆矩阵绘制:')
test_labels, test_preds = collect_pred_labels(model, testloader, device)
cm_test = confusion_matrix(test_labels, test_preds)
plot_confusion_matrix(cm=cm_test,
class_names=classes,
title='Test Set Confusion Matrix',
img_name='test_set')
# ======================== 绘制混淆矩阵结束 =====================
def display_loss_curve(history: dict):
"""
绘制历史的训练损失和准确率的折线图
:param history: dict, {"train_loss":[loss values], "train_accuracy":[accuracy values]}
:return: none
"""
# 转为 DF,方便送入 seaborn
df = pd.DataFrame(history)
df['epoch'] = range(1, len(df)+1)
sns.set_style('darkgrid')
fig, ax = plt.subplots(1,2,figsize=(10,5))
# 绘制训练损失
sns.lineplot(
data=df,
x='epoch',
y='train_loss',
ax=ax[0],
color='b',
marker='o'
)
# 在坐标点上打印文字
for index,row in df.iterrows():
ax[0].text(
row['epoch'],
row['train_loss'],
f"{row['train_loss']:.3f}",
ha='center',
va='bottom',
fontsize=10,
color='k'
)
ax[0].set_title('Train Loss With Softmax')
ax[0].set_xlabel('Epoch')
ax[0].set_ylabel('Loss')
# 绘制训练准确率
sns.lineplot(
data=df,
x='epoch',
y='train_accuracy',
color='r',
marker='o'
)
for index,row in df.iterrows():
ax[1].text(
row['epoch'],
row['train_accuracy'],
f"{row['train_accuracy']:.3f}",
ha='center',
va='bottom',
fontsize=10,
color='k'
)
ax[1].set_title('Train Accuracy With Softmax')
ax[1].set_xlabel('Epoch')
ax[1].set_ylabel('Accuracy')
plt.tight_layout()
plt.savefig('with_softmax_net_loss.png',dpi=300)
plt.show()
def valiation(PATH):
"""评估模块"""
# =============== 评估部分 =====================
# 简单的图像评估区块
# 使用已持久化模型进行评估
model = Net()
model.load_state_dict(torch.load(PATH, weights_only=True))
print('加载模型成功')
# def imshow(img):
# img = img / 2 + 0.5 # 反标准化
# npimg = img.numpy()
# plt.imshow(np.transpose(npimg, (1, 2, 0)))
# plt.show()
#
# data_iter = iter(testloader)
# images, labels = next(data_iter)
#
# show_images = 8
# images_to_show = images[:show_images]
# labels_to_show = labels[:show_images]
#
# print('GroundTruth: ', ' '.join(f'{classes[labels_to_show[j]]:5s}' for j in range(show_images)))
# # 预测标签
# with torch.no_grad():
# outputs = model(images_to_show)
# _, predicted = torch.max(outputs, 1)
# print('Predicted: ', ' '.join(f'{classes[predicted[j]]:5s}' for j in range(show_images)))
#
# imshow(torchvision.utils.make_grid(images_to_show))
# 模型评估区块 (在测试集上评估)
# def pred_model(model, testloader, loss_function, device):
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
test_accuracy = pred_model_in_testset(
model=model,
testloader=testloader,
device=device
)
print(f'测试集准确率:{test_accuracy * 100:.2f}%')
# 具体分类评估区块:
# 在每一个分类上进行评估,观察每一个分类的准确率
# 从已持久化模型加载模型
correct_pred = {classname: 0 for classname in classes}
total_pred = {classname: 0 for classname in classes}
with torch.no_grad():
for data in testloader:
images, labels = data[0].to(device), data[1].to(device)
outputs = model(images)
_, predictions = torch.max(outputs, 1)
# 累加每个类别的准确率计算变量
for label, prediction in zip(labels, predictions):
if label == prediction:
correct_pred[classes[label]] += 1
total_pred[classes[label]] += 1
for classname, correct_count in correct_pred.items():
accuracy = 100 * float(correct_count) / total_pred[classname]
print(f'Class: {classname:5s} Accuracy: {accuracy:.1f} %')
# ============== 评估部分结束 ==================
def train_model(PATH):
# 训练设备选择区块
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
print(f'选择训练的设备:{device}')
print(f'开始构建神经网络:')
model = Net()
print('神经网络结构:')
print(model)
print('神经网络构建完成')
# 神经网络训练区块
print('开始训练神经网络:')
# 1.定义损失函数
loss_function = nn.CrossEntropyLoss()
# 2.定义优化器
optimizer = optim.Adam(model.parameters(), lr=0.001)
# 3.传入训练函数
# def train(model, device, trainloader, loss_function, optimizer, epoches):
# 使用 tensorboard 可视化训练过程
from torch.utils.tensorboard import SummaryWriter
writer = SummaryWriter('./logs')
trained_model,history = train(
model=model,
device=device,
trainloader=trainloader,
loss_function=loss_function,
optimizer=optimizer,
epoches=10,
writer=writer
)
writer.close()
print('结束Summary的写入')
# 存储训练数据
import json
file_path = 'train_with_softmax.json'
with open(file_path, 'w') as f:
json.dump(history, f, indent=4, ensure_ascii=False)
# 模型持久化区块
save_model(trained_model,PATH)
if __name__ == '__main__':
transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
# 超参数定义区块
batch_size = 256
# 数据加载区块
trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=batch_size,
shuffle=True, num_workers=get_dataloader_workers())
testset = torchvision.datasets.CIFAR10(root='./data', train=False,
download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=batch_size,
shuffle=False, num_workers=get_dataloader_workers())
classes = ('plane', 'car', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
# 模型训练函数
# train_model(PATH='./CIFAR_with_softmax.pth')
# 模型预测和验证函数
# valiation(PATH='./CIFAR_with_softmax.pth')
# # 损失曲线绘制函数
# import json
# file_path = 'train_with_softmax.json'
# with open(file_path, "r", encoding="utf-8") as f:
# history = json.load(f)
#
# display_loss_curve(history=history)